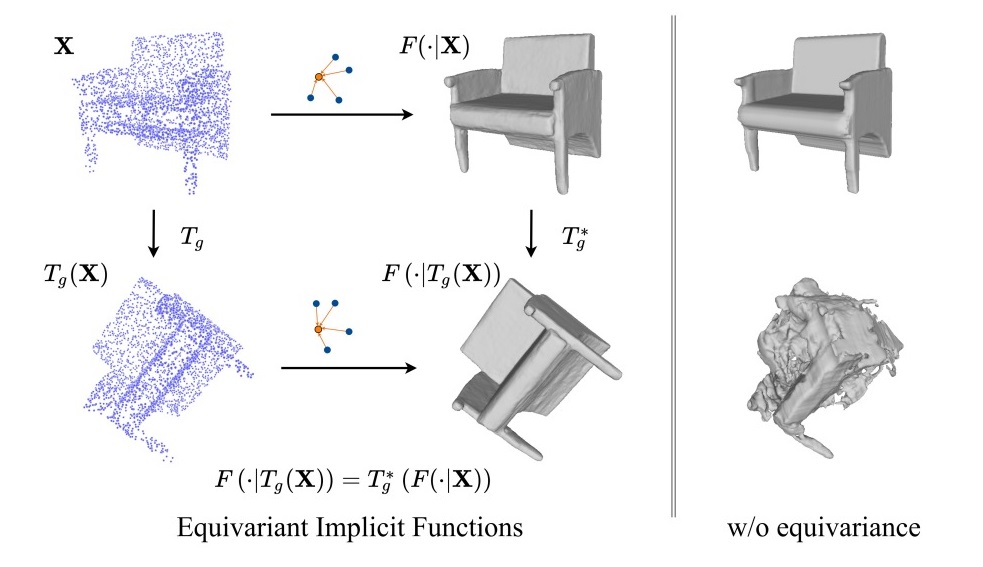
In recent years, neural implicit representations have made remarkable progress in modeling of 3D shapes with arbitrary topology. In this work, we address two key limitations of such representations, in failing to capture local 3D geometric fine details, and to learn from and generalize to shapes with unseen 3D transformations. To this end, we introduce a novel family of graph implicit functions with equivariant layers that facilitates modeling fine local details and guaranteed robustness to various groups of geometric transformations, through local k-NN graph embeddings with sparse point set observations at multiple resolutions. Our method improves over the existing rotation-equivariant implicit function from 0.69 to 0.89 (IoU) on the ShapeNet reconstruction task. We also show that our equivariant implicit function can be extended to other types of similarity transformations and generalizes to unseen translations and scaling.

Paper

Bibtex