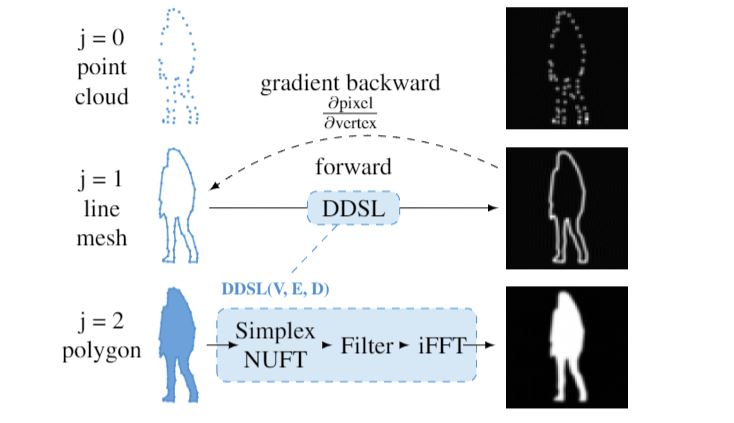
We present a Deep Differentiable Simplex Layer (DDSL)for neural networks for geometric deep learning. The DDSL is a differentiable layer compatible with deep neural networks for bridging simplex mesh-based geometry representations (point clouds, line mesh, triangular mesh, tetrahedral mesh) with raster images (e.g., 2D/3D grids). The DDSL uses Non-Uniform Fourier Transform (NUFT) toperform differentiable, efficient, anti-aliased rasterization of simplex-based signals. We present a complete theoretical framework for the process as well as an efficient backpropagation algorithm. Compared to previous differentiable renderers and rasterizers, the DDSL generalizes to arbitrary simplex degrees and dimensions. In particular, we exploreits applications to 2D shapes and illustrate two applicationsof this method: (1) mesh editing and optimization guided by neural network outputs, and (2) using DDSL for a differentiable rasterization loss to facilitate end-to-end training ofpolygon generators. We are able to validate the effectiveness of gradient-based shape optimization with the example of airfoil optimization, and using the differentiable rasterization loss to facilitate end-to-end training, we surpass state of the art for polygonal image segmentation given ground-truth bounding boxes.

Bibtex

Google Scholar